Cos 2x Sin 2x Sinx
letscamok
Sep 07, 2025 · 6 min read
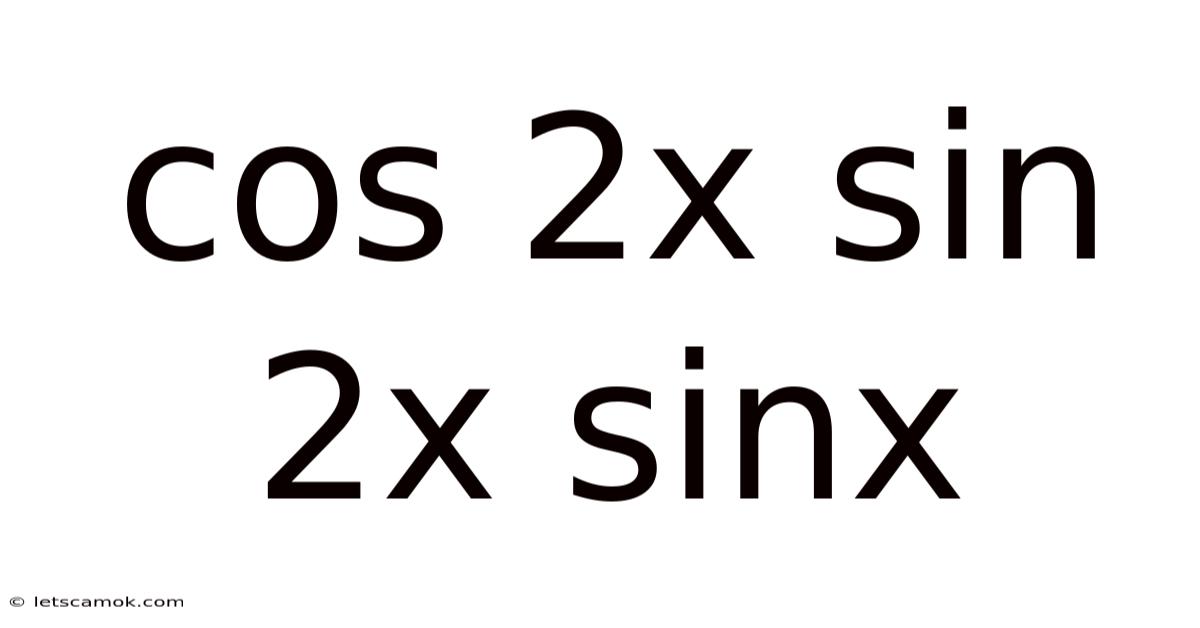
Table of Contents
Decoding the Trigonometric Expression: cos 2x sin 2x sin x
Understanding trigonometric identities and their applications is crucial for success in mathematics, particularly in calculus, physics, and engineering. This article delves into the intricacies of the trigonometric expression cos 2x sin 2x sin x, exploring its simplification, potential applications, and providing a comprehensive understanding suitable for students and enthusiasts alike. We'll unravel its complexities step-by-step, employing various trigonometric identities to reach a simplified form and highlighting the underlying mathematical principles involved.
Introduction: Unveiling the Complexity
The expression cos 2x sin 2x sin x appears deceptively simple at first glance. However, its inherent complexity stems from the interplay of multiple angles (x, 2x) and the mixture of sine and cosine functions. To effectively analyze and simplify this expression, we will leverage fundamental trigonometric identities, including double-angle formulas and product-to-sum formulas. This journey will not only simplify the expression but also enhance our understanding of trigonometric manipulation techniques. The ultimate goal is to express this seemingly complicated expression in a more manageable and insightful form, potentially revealing underlying patterns and relationships.
Step-by-Step Simplification: A Journey Through Trigonometric Identities
Our approach involves a systematic simplification process using well-established trigonometric identities. Let's embark on this journey step-by-step:
Step 1: Utilizing Double-Angle Formulas
We begin by applying the double-angle formulas for sine and cosine:
- sin 2x = 2 sin x cos x
- cos 2x = cos²x - sin²x (or alternatively, 2cos²x - 1, or 1 - 2sin²x)
Substituting these into our original expression, we get:
(cos²x - sin²x)(2 sin x cos x)(sin x)
Step 2: Rearranging and Factoring
Let's rearrange the terms for better clarity and factoring opportunities:
2 sin²x cos x (cos²x - sin²x)
We can further factor out a cos x:
2 sin²x cos x (cos x - sin x)(cos x + sin x)
Step 3: Exploring Alternative Approaches
While the above simplification is valid, we can explore alternative paths using different double-angle formulas for cos 2x. Let's use cos 2x = 1 - 2sin²x:
(1 - 2sin²x)(2 sin x cos x)(sin x)
This leads to:
2 sin²x cos x (1 - 2sin²x)
This expression, while simplified, doesn't offer a significantly more compact form than the previous result. The choice between these simplified forms depends on the context of the problem and the desired form for further manipulations.
Step 4: Considering Product-to-Sum Formulas
Another avenue for simplification involves utilizing product-to-sum formulas. However, in this case, applying product-to-sum directly to the original expression might lead to a more complex intermediate result. The factorized forms obtained in Steps 2 and 3 are generally preferred for their relative simplicity and suitability for further analysis or applications.
Mathematical Insights and Applications
The simplified expressions obtained (2 sin²x cos x (cos²x - sin²x) or 2 sin²x cos x (1 - 2sin²x)) offer valuable insights:
- Dependence on x: The expression's value entirely depends on the value of x. Understanding the behavior of sine and cosine functions allows us to predict the behavior of this expression across different values of x.
- Zeros and Extrema: Setting the simplified expression to zero helps determine the values of x where the expression equals zero. Analyzing the derivative of the expression can reveal its maxima and minima.
- Periodicity: Since the expression involves sine and cosine functions, it will exhibit periodicity. The period of the expression will be related to the periods of the individual sine and cosine functions involved.
- Graphical Representation: Plotting the simplified expression against x provides a visual representation of its behavior, revealing its periodic nature, zeros, and extrema. This graphical representation enhances our understanding of the expression's characteristics.
The simplification of cos 2x sin 2x sin x is not just an academic exercise. This type of manipulation is crucial in:
- Solving Trigonometric Equations: Simplifying complex expressions helps in solving trigonometric equations, where finding the values of x that satisfy a given equation is the objective.
- Calculus: In calculus, simplifying trigonometric expressions is essential for evaluating integrals and derivatives involving trigonometric functions. This simplification often makes integration or differentiation significantly easier.
- Physics and Engineering: Many physical phenomena are modeled using trigonometric functions. Simplifying such expressions is crucial for analyzing and solving problems in fields like wave mechanics, oscillations, and signal processing.
Frequently Asked Questions (FAQ)
Q1: Are there other ways to simplify cos 2x sin 2x sin x?
A1: While the methods outlined above provide effective simplification, other approaches exist. One could utilize other trigonometric identities, or a combination of identities, to achieve a slightly different, yet equally valid, simplified form. However, the key is to choose the approach that leads to the most manageable and insightful expression for the specific problem at hand.
Q2: What is the significance of factoring in this simplification?
A2: Factoring plays a critical role in simplification because it allows us to express the expression in a more compact and revealing form. Factoring helps identify common factors, potentially revealing underlying patterns and relationships that might not be apparent in the original, expanded form. It also simplifies further manipulation or analysis of the expression.
Q3: How can I verify the simplified expressions?
A3: Verification can be done by substituting specific values of x into both the original expression and the simplified versions. If both expressions yield the same result for various values of x, it strongly suggests that the simplification is correct. Furthermore, using a graphing calculator or software to plot both expressions can visually confirm their equivalence.
Q4: What if the expression involved different multiples of x, such as cos 3x sin 4x sin x?
A4: For expressions involving different multiples of x, a similar approach can be used. However, the simplification process will likely be more complex, requiring a judicious selection and application of appropriate trigonometric identities, including multiple-angle formulas and product-to-sum formulas. The complexity increases with the number of angles and the variety of trigonometric functions involved.
Conclusion: Mastering Trigonometric Simplification
The simplification of cos 2x sin 2x sin x demonstrates the power and elegance of trigonometric identities. By systematically applying these identities, we transformed a seemingly complex expression into more manageable forms, revealing underlying patterns and enhancing our understanding of its behavior. This process not only hones our algebraic manipulation skills but also provides essential tools for tackling more complex problems in mathematics, science, and engineering. Remember that the choice of simplification method often depends on the context of the problem and the desired form for further applications. Through practice and exploration of different approaches, one can master the art of trigonometric simplification and appreciate its significant role in various mathematical and scientific disciplines. The key takeaway is to approach such problems with a systematic method, leverage your knowledge of trigonometric identities strategically, and always verify your results.
Latest Posts
Latest Posts
-
Keys On A Keyboard Computer
Sep 08, 2025
-
Year 7 Maths Test Papers
Sep 08, 2025
-
Physics Required Practicals Paper 1
Sep 08, 2025
-
Spencer Arms Pub Chapel Brampton
Sep 08, 2025
-
What Is A Butterfly Stitch
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Cos 2x Sin 2x Sinx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.