Sin X Sin 180 X
letscamok
Sep 24, 2025 · 6 min read
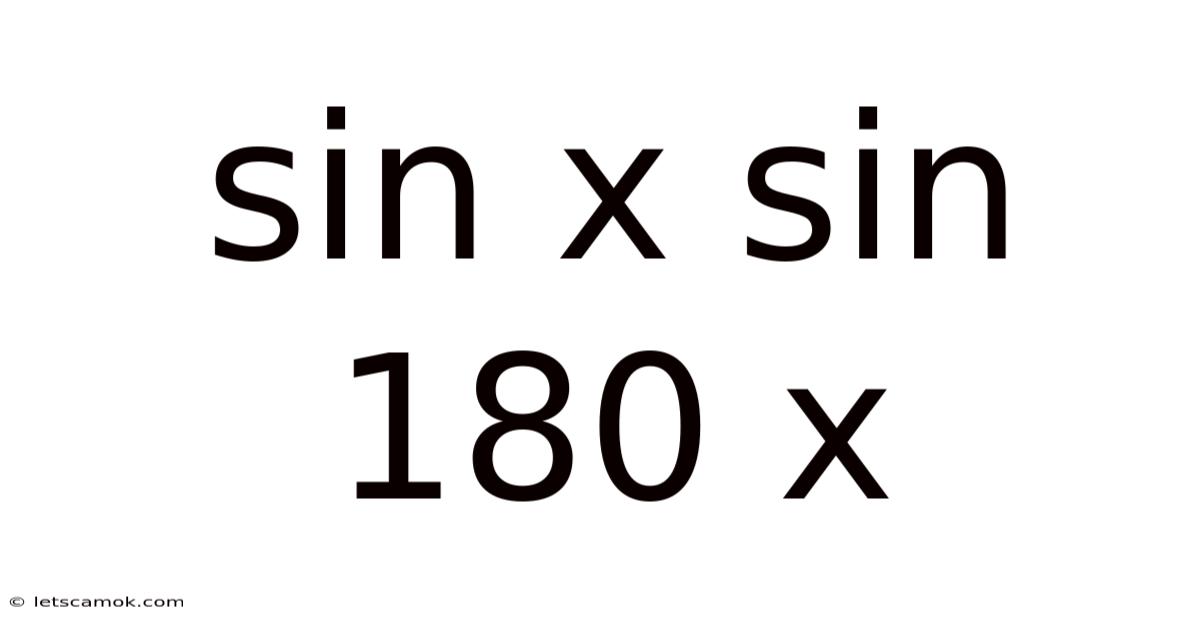
Table of Contents
Unveiling the Mystery of sin x sin 180° - x: A Deep Dive into Trigonometric Identities
Understanding trigonometric identities is fundamental to mastering mathematics, particularly in fields like calculus, physics, and engineering. This article delves into the intriguing relationship between sin x and sin(180° - x), exploring its derivation, applications, and significance within the broader context of trigonometry. We will dissect this identity, providing a comprehensive explanation suitable for students and enthusiasts alike, while ensuring the content is search engine optimized and engaging. The core concept of this article revolves around understanding the sine function, trigonometric identities, and their practical applications.
Introduction: Navigating the World of Angles and Sine
The sine function, a cornerstone of trigonometry, relates an angle of a right-angled triangle to the ratio of the length of the side opposite the angle to the length of the hypotenuse. While initially defined within the context of right-angled triangles, its application expands to encompass all angles, positive and negative, through the use of the unit circle. Understanding the behavior of the sine function across different quadrants is crucial for comprehending trigonometric identities. This article focuses on a specific identity: sin x = sin(180° - x). This seemingly simple equation holds profound implications and unlocks numerous problem-solving techniques within trigonometry and beyond.
Understanding the Unit Circle and Sine's Behavior
Before diving into the proof, let's visualize the sine function using the unit circle. The unit circle is a circle with a radius of 1, centered at the origin of a coordinate plane. Any point on the unit circle can be represented by its coordinates (cos θ, sin θ), where θ is the angle formed between the positive x-axis and the line connecting the origin to the point.
The sine of an angle θ is the y-coordinate of the point on the unit circle corresponding to that angle. Observe the following:
- First Quadrant (0° to 90°): Both sine and cosine are positive.
- Second Quadrant (90° to 180°): Sine is positive, cosine is negative.
- Third Quadrant (180° to 270°): Both sine and cosine are negative.
- Fourth Quadrant (270° to 360°): Sine is negative, cosine is positive.
This understanding of the signs of sine in different quadrants is pivotal in grasping the identity sin x = sin(180° - x).
Proof of the Identity: sin x = sin(180° - x)
We can prove this identity using several approaches. One elegant method involves using the sine subtraction formula:
sin(A - B) = sin A cos B - cos A sin B
Let A = 180° and B = x. Substituting these values into the formula, we get:
sin(180° - x) = sin 180° cos x - cos 180° sin x
We know that sin 180° = 0 and cos 180° = -1. Substituting these values:
sin(180° - x) = (0) cos x - (-1) sin x
sin(180° - x) = sin x
This elegantly demonstrates the identity.
Visualizing the Identity: A Geometric Approach
Consider a unit circle. Let's mark an angle 'x' in the first quadrant. The y-coordinate of the point on the circle corresponding to angle 'x' represents sin x. Now, consider the angle (180° - x). This angle lies in the second quadrant. Notice that the y-coordinate of the point corresponding to (180° - x) is the same as the y-coordinate of the point corresponding to 'x'. This geometrical representation reinforces the fact that sin x = sin(180° - x). This visual proof solidifies the understanding of the identity, making it more intuitive and less abstract.
Applications of the Identity: Problem Solving and Simplification
The identity sin x = sin(180° - x) is a powerful tool in solving trigonometric equations and simplifying complex expressions. Its applications extend to various areas, including:
-
Solving Trigonometric Equations: This identity allows us to find additional solutions to trigonometric equations. For instance, if sin x = 0.5, one solution is x = 30°. Using the identity, we can find another solution: x = 180° - 30° = 150°. This highlights how the identity helps us identify all possible solutions within a given range.
-
Simplifying Trigonometric Expressions: This identity can be used to simplify complex trigonometric expressions by replacing sin(180° - x) with sin x, streamlining calculations and making problem-solving more efficient.
-
Calculus: In calculus, understanding this identity is crucial for evaluating integrals and derivatives of trigonometric functions. It allows for manipulation and simplification of expressions, leading to easier solutions.
-
Physics and Engineering: Numerous applications in physics and engineering involve sinusoidal functions, representing oscillations, waves, and alternating currents. The identity provides a crucial tool for analyzing and manipulating these functions.
Expanding the Understanding: Generalizations and Related Identities
The identity sin x = sin(180° - x) is a specific instance of a broader family of identities. Understanding this broader context enhances one's grasp of trigonometric relationships.
-
Sine in other quadrants: Similar identities can be derived for other quadrants, reflecting the symmetry and periodicity of the sine function. For example, sin(360° + x) = sin x, reflecting the 360° periodicity.
-
Cosine and Tangent Identities: Similar identities exist for cosine and tangent functions, revealing the intricate relationships between these trigonometric functions. Understanding these related identities provides a more holistic picture of trigonometric relationships.
Frequently Asked Questions (FAQ)
Q: Is this identity valid for all values of x?
A: Yes, this identity holds true for all real values of x.
Q: How does this identity relate to the concept of reference angles?
A: The identity highlights the concept of reference angles. The reference angle is the acute angle formed between the terminal side of an angle and the x-axis. The sine of an angle and its reference angle have the same magnitude, differing only in sign depending on the quadrant.
Q: Can I use this identity with radians instead of degrees?
A: Absolutely! The identity remains valid if you use radians. The equivalent identity in radians is sin x = sin(π - x).
Q: Are there any limitations to using this identity?
A: While the identity is generally applicable, always ensure you are working within the correct domain and range for sine functions, especially when solving equations involving inverse trigonometric functions.
Conclusion: Mastering Trigonometric Identities for Enhanced Mathematical Proficiency
The identity sin x = sin(180° - x) is a fundamental trigonometric identity with far-reaching implications. Understanding its derivation, visualization, and applications is crucial for mastering trigonometry and successfully navigating related fields. This identity is not merely a mathematical fact; it's a key that unlocks deeper understanding and facilitates problem-solving in numerous contexts. By understanding this identity and its broader implications, students and enthusiasts can enhance their mathematical skills and appreciate the elegant interconnectedness within the world of trigonometry. Through continuous practice and exploration, mastering trigonometric identities like this one lays a solid foundation for tackling more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Anuyu Hair And Beauty Salon
Sep 24, 2025
-
What Do Orbs Look Like
Sep 24, 2025
-
Do Honey Bees Eat Honey
Sep 24, 2025
-
Canal Boats For Sale Yorkshire
Sep 24, 2025
-
Aqa Physics Gcse Past Papers
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Sin X Sin 180 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.