Sin X Cos X Integral
letscamok
Sep 12, 2025 · 6 min read
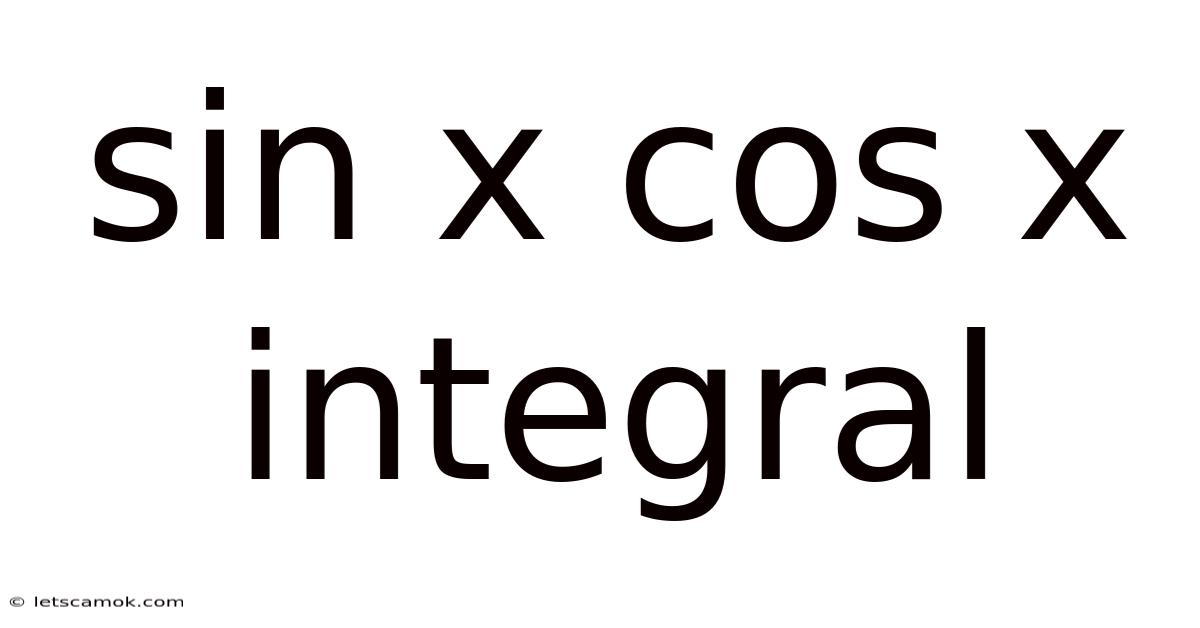
Table of Contents
Mastering the Integral of sin x cos x: A Comprehensive Guide
The integral of sin x cos x is a fundamental concept in calculus, frequently encountered in various applications, from physics and engineering to computer graphics and signal processing. This comprehensive guide will walk you through different methods of solving this integral, delve into its underlying principles, and explore its practical applications. Understanding this integral is crucial for mastering more complex trigonometric integrations. We'll cover everything from basic trigonometric identities to advanced techniques, ensuring a thorough understanding for students of all levels.
Introduction: Understanding the Problem
The problem we're tackling is evaluating the indefinite integral: ∫sin x cos x dx. This seemingly simple integral presents multiple pathways to its solution, each offering valuable insights into integral calculus techniques. We'll explore several methods, highlighting their advantages and disadvantages. The key to solving this, and many other trigonometric integrals, lies in the skillful application of trigonometric identities and substitution techniques.
Method 1: Using the Double Angle Identity
One of the most straightforward methods utilizes the double angle identity for sine. Recall the identity: sin(2x) = 2sin x cos x. This allows us to rewrite the integrand as:
∫sin x cos x dx = (1/2) ∫sin(2x) dx
Now, the integral becomes significantly easier to solve. We can use a simple u-substitution:
Let u = 2x, then du = 2dx, and dx = (1/2)du
Substituting into our integral:
(1/2) ∫sin(u) (1/2) du = (1/4) ∫sin(u) du
The integral of sin(u) is -cos(u). Therefore:
(1/4) ∫sin(u) du = -(1/4)cos(u) + C
Substituting back for u = 2x:
-(1/4)cos(2x) + C
Therefore, the integral of sin x cos x using the double angle identity is -(1/4)cos(2x) + C, where C is the constant of integration.
Method 2: Using Integration by Parts
Integration by parts is a powerful technique applicable to a wide range of integrals. It's based on the product rule for differentiation: d(uv) = u dv + v du. Rearranging this gives the integration by parts formula:
∫u dv = uv - ∫v du
Let's apply this to our integral:
Let u = sin x, then du = cos x dx Let dv = cos x dx, then v = sin x
Applying the integration by parts formula:
∫sin x cos x dx = sin x * sin x - ∫sin x cos x dx
Notice that the integral we started with appears on both sides of the equation. This might seem problematic, but we can solve for the integral:
2∫sin x cos x dx = sin²x ∫sin x cos x dx = (1/2)sin²x + C
This seems to give us a different answer than Method 1. However, remember that trigonometric identities relate these expressions. Using the double-angle identity for cosine, cos(2x) = 1 - 2sin²x, we can rewrite sin²x as (1 - cos(2x))/2. Substituting this into our result:
(1/2)sin²x + C = (1/2)[(1 - cos(2x))/2] + C = (1/4)(1 - cos(2x)) + C = (1/4) - (1/4)cos(2x) + C
The constant (1/4) gets absorbed into the constant of integration, giving us the same result as Method 1: -(1/4)cos(2x) + C. This demonstrates the equivalence of the two methods.
Method 3: Using a Simple Substitution
A more direct substitution method can also be employed. Let's try the substitution:
Let u = sin x, then du = cos x dx
Our integral becomes:
∫u du = (1/2)u² + C
Substituting back for u = sin x:
(1/2)sin²x + C
Again, this appears different but is equivalent to the previous solutions using trigonometric identities, as shown above.
Comparing the Methods
All three methods yield equivalent results, although they may appear different at first glance. The double angle identity method is generally considered the most efficient and straightforward for this specific integral. Integration by parts, while a powerful technique, adds an extra layer of complexity in this case. The simple substitution method, although successful, is less intuitive than the double angle approach. The choice of method often depends on personal preference and the context of the larger problem.
The Significance of the Constant of Integration (C)
It's crucial to remember the constant of integration, denoted by 'C', in each solution. This constant represents the family of curves whose derivatives are sin x cos x. Without the constant, the solution is incomplete and doesn't represent the entire set of antiderivatives. The value of 'C' can only be determined if specific boundary conditions or initial values are provided.
Definite Integrals and Applications
While we've focused on the indefinite integral, the results are easily applied to definite integrals. If we want to evaluate the integral of sin x cos x over a specific interval [a, b], we would compute:
∫(from a to b) sin x cos x dx = = -(1/4)cos(2b) + (1/4)cos(2a)
This definite integral finds applications in numerous fields:
- Physics: Calculating work done by a variable force, determining the displacement of an object under varying acceleration.
- Engineering: Analyzing oscillating systems, computing areas under curves representing physical quantities.
- Computer Graphics: Modeling wave phenomena, creating realistic animations.
- Signal Processing: Analyzing and manipulating periodic signals.
Extending the Concept: Integrals of Similar Forms
Understanding the integral of sin x cos x lays the foundation for solving more complex integrals involving products of trigonometric functions. For instance, integrals of the form ∫sinⁿx cosᵐx dx can be tackled using techniques like reduction formulas or further trigonometric substitutions, depending on the values of n and m.
Frequently Asked Questions (FAQ)
Q: Can I use other trigonometric identities to solve this integral?
A: Yes, you can utilize other identities, but the double angle identity often provides the most direct path to a solution. However, exploring alternative methods can deepen your understanding of trigonometric relationships.
Q: What if the integral involves sin(ax)cos(bx)?
A: This requires the use of product-to-sum formulas, which express the product of sine and cosine functions as a sum of sine or cosine functions. These formulas allow you to rewrite the integrand into a form that is easily integrable.
Q: Why is the constant of integration important?
A: The constant of integration represents the family of functions that share the same derivative. Omitting it leads to an incomplete and inaccurate solution. Only when boundary conditions are provided can a specific value for the constant be determined.
Q: How can I check my answer?
A: The best way to check your answer is to differentiate your result. If the derivative matches the original integrand, your solution is correct.
Q: Are there any numerical methods for approximating this integral?
A: Yes, numerical methods like the trapezoidal rule or Simpson's rule can provide approximate solutions, especially for integrals that are difficult to solve analytically. However, for this specific integral, the analytical solutions are readily available and preferable.
Conclusion: Mastering Trigonometric Integration
The integral of sin x cos x, seemingly straightforward, offers a valuable learning opportunity to apply various integration techniques and strengthen your understanding of trigonometric identities. Mastering this integral forms a cornerstone for tackling more complex trigonometric integrations that are prevalent in various scientific and engineering disciplines. By understanding the multiple approaches and their underlying principles, you can confidently navigate similar problems and further enhance your calculus skills. Remember to always check your work, consider the context of the problem, and appreciate the power and elegance of calculus in solving real-world problems.
Latest Posts
Latest Posts
-
Son Tattoo Quotes For Mom
Sep 12, 2025
-
Where Is Madeira Cake From
Sep 12, 2025
-
Clive Barker Thief Of Always
Sep 12, 2025
-
In Flanders Fields Poem Meaning
Sep 12, 2025
-
Singing The Faith Hymn Book
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Sin X Cos X Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.