Integration Of X Sin X
letscamok
Sep 08, 2025 · 5 min read
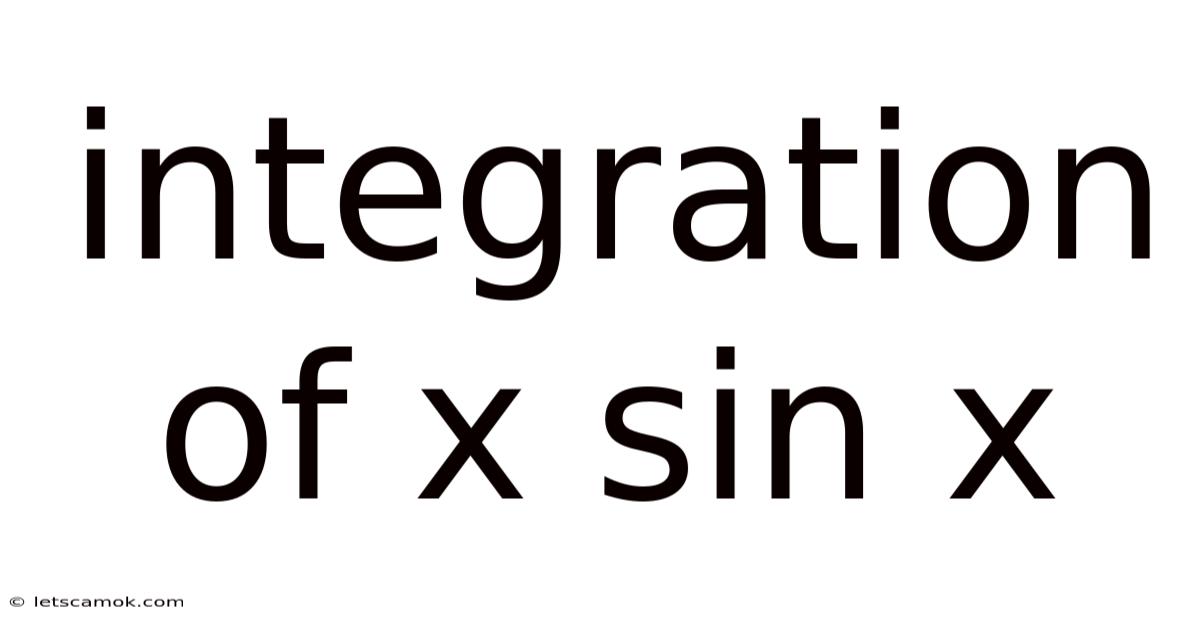
Table of Contents
Integrating x sin x: A Comprehensive Guide
Integrating x sin x is a common problem encountered in calculus courses and various applications of mathematics in science and engineering. This seemingly simple integral requires a specific technique, and understanding its solution unlocks a deeper understanding of integration by parts. This article will provide a comprehensive guide, exploring the method, its underlying principles, and various related considerations. We will move beyond a simple solution to delve into the 'why' and 'how' to solidify your understanding.
Introduction: Understanding the Challenge
The integral ∫x sin x dx isn't directly solvable using standard integration rules. Unlike simple polynomial or trigonometric functions, this integral involves a product of two distinct functions: a polynomial function (x) and a trigonometric function (sin x). This is where the powerful technique of integration by parts comes into play. This method is crucial for integrating products of functions and forms the backbone of solving this particular integral. Mastering integration by parts is essential for anyone looking to advance their calculus skills.
Integration by Parts: The Core Technique
Integration by parts is a powerful technique derived from the product rule for differentiation. The product rule states: d(uv) = u dv + v du. By rearranging and integrating both sides, we arrive at the formula for integration by parts:
∫u dv = uv - ∫v du
Choosing the right 'u' and 'dv' is crucial for successful application. The common mnemonic LIATE can help:
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions (like polynomials)
- Trigonometric functions
- Exponential functions
The order suggests prioritizing functions higher on the list as 'u'. In our case, x sin x, 'x' (algebraic) is prioritized over 'sin x' (trigonometric).
Step-by-Step Solution of ∫x sin x dx
-
Identify u and dv:
- Let u = x. Then du = dx.
- Let dv = sin x dx. Then v = -cos x (integrating dv).
-
Apply the Integration by Parts Formula:
∫x sin x dx = uv - ∫v du = x(-cos x) - ∫(-cos x) dx
-
Simplify and Integrate:
= -x cos x + ∫cos x dx = -x cos x + sin x + C
Where 'C' is the constant of integration. This constant is essential because the derivative of a constant is zero, meaning many functions could have the same derivative.
Therefore, the solution to ∫x sin x dx is -x cos x + sin x + C.
Delving Deeper: Why This Method Works
The success of integration by parts hinges on cleverly transforming a complex integral into a simpler one. By choosing 'u' and 'dv' strategically, we aim to make the integral ∫v du easier to solve than the original ∫u dv. In our example, the original integral involves the product of x and sin x. By selecting u = x, we reduced it to ∫-cos x dx, which is a straightforward integration. The choice of 'u' and 'dv' is not always obvious and sometimes requires practice and intuition.
Exploring Variations: ∫x² sin x dx and Beyond
The technique extends beyond simple x sin x. Let's consider ∫x² sin x dx. Here, we'll need to apply integration by parts twice:
-
First Application:
- u = x², du = 2x dx
- dv = sin x dx, v = -cos x
∫x² sin x dx = -x² cos x + ∫2x cos x dx
-
Second Application:
- u = 2x, du = 2 dx
- dv = cos x dx, v = sin x
∫2x cos x dx = 2x sin x - ∫2 sin x dx = 2x sin x + 2 cos x + C
-
Combining Results:
∫x² sin x dx = -x² cos x + 2x sin x + 2 cos x + C
This demonstrates the iterative nature of integration by parts. For higher powers of x (e.g., x³, x⁴ sin x), the process would require more iterations. Each application simplifies the polynomial part, eventually leading to a solvable integral.
Applications in Science and Engineering
The ability to integrate functions like x sin x is not merely a theoretical exercise. It has significant practical applications in various fields:
- Physics: Solving differential equations that model oscillatory systems, such as damped harmonic oscillators.
- Engineering: Calculating Fourier transforms, crucial in signal processing and communications.
- Probability and Statistics: Evaluating expected values of certain probability distributions.
These applications highlight the importance of mastering techniques like integration by parts.
Frequently Asked Questions (FAQ)
-
Q: What if I choose 'u' and 'dv' differently? A: While the LIATE rule provides guidance, other choices might work. However, an incorrect choice can lead to a more complex integral, or even an integral that's unsolvable using this method. It's a matter of finding the most efficient path.
-
Q: Can I use other integration techniques here? A: While substitution might seem applicable initially, it won't effectively solve this type of integral. Integration by parts is specifically designed for integrating products of functions.
-
Q: How do I check my answer? A: Differentiate your answer. If the derivative matches the original integrand (x sin x), your solution is correct.
-
Q: What if I encounter more complicated integrands? A: For even more complex integrals involving products of functions, advanced techniques might be required, such as integration tables or numerical methods.
Conclusion: Mastering a Fundamental Calculus Skill
Successfully integrating x sin x, and similar functions, requires understanding and mastering integration by parts. This technique is a cornerstone of calculus, empowering you to solve a wide range of integrals beyond those solvable with basic rules. This article not only provides the solution but also delves into the underlying logic, illustrating its power and versatility. The step-by-step examples and explanations aim to equip you with the confidence and skills needed to tackle similar problems, advancing your understanding of integral calculus and its wide-ranging applications in various scientific and engineering domains. The iterative nature of the process for more complex problems like ∫xⁿ sin x dx highlights the elegance and effectiveness of this powerful method, solidifying your understanding of calculus as a fundamental tool for problem-solving. Remember to practice and reinforce your skills; mastery comes with consistent effort and a deep understanding of the underlying principles.
Latest Posts
Latest Posts
-
What Is Leading In Typography
Sep 08, 2025
-
Case Study Of Hm Psychology
Sep 08, 2025
-
Working At Height Toolbox Talk
Sep 08, 2025
-
Stave 1 Christmas Carol Quotes
Sep 08, 2025
-
Roles And Responsibilities Of Educators
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about Integration Of X Sin X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.