Integration Of Sin Squared X
letscamok
Sep 10, 2025 · 5 min read
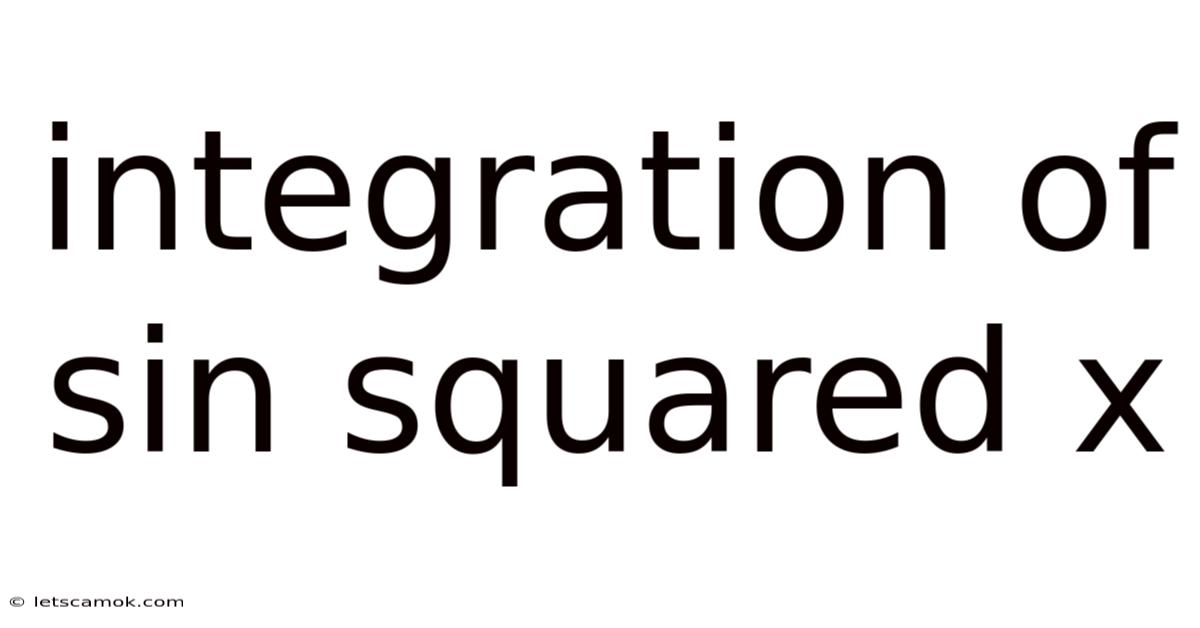
Table of Contents
Mastering the Integration of Sin²x: A Comprehensive Guide
The integration of trigonometric functions is a cornerstone of calculus, frequently appearing in physics, engineering, and other scientific fields. While seemingly straightforward, integrating trigonometric functions often requires clever manipulation and the application of various trigonometric identities. This comprehensive guide will delve into the intricacies of integrating sin²x, exploring different methods and providing a deep understanding of the underlying principles. We'll cover various approaches, explain the underlying mathematical logic, and address common questions and misconceptions. By the end, you'll be confident in tackling this seemingly challenging integral.
Understanding the Challenge: Why isn't it Simply -cos²x?
A common initial mistake is to assume the integral of sin²x is simply -cos²x. This is incorrect. The derivative of cos²x involves the chain rule, resulting in a factor of -2cosxsinx, not simply sin²x. Therefore, a different strategy is required. This necessitates utilizing trigonometric identities to transform the integrand into a more manageable form.
Method 1: Using the Power-Reducing Formula
This method leverages a fundamental trigonometric identity to simplify the integrand. The power-reducing formula for sin²x is:
sin²x = (1 - cos(2x))/2
By substituting this identity into the integral, we obtain a much simpler expression:
∫sin²x dx = ∫(1 - cos(2x))/2 dx
This integral can now be easily solved using basic integration rules:
∫(1 - cos(2x))/2 dx = (1/2)∫(1 - cos(2x)) dx = (1/2) [∫1 dx - ∫cos(2x) dx]
The integral of 1 with respect to x is simply x. The integral of cos(2x) requires a simple u-substitution:
Let u = 2x, then du = 2dx, and dx = du/2
Therefore, ∫cos(2x) dx = (1/2)∫cos(u) du = (1/2)sin(u) = (1/2)sin(2x)
Substituting back into our original equation, we get:
∫sin²x dx = (1/2)[x - (1/2)sin(2x)] + C
Where C is the constant of integration. This can be further simplified to:
∫sin²x dx = x/2 - (1/4)sin(2x) + C
This is the final, simplified solution obtained using the power-reducing formula. This method is generally preferred for its simplicity and direct application of a well-known identity.
Method 2: Integration by Parts
While less efficient than the power-reducing formula method, integration by parts provides an alternative approach and demonstrates a broader application of integration techniques. The integration by parts formula is:
∫u dv = uv - ∫v du
Let's apply this to ∫sin²x dx. We can cleverly choose:
- u = sinx, then du = cosx dx
- dv = sinx dx, then v = -cosx
Substituting these into the integration by parts formula:
∫sin²x dx = sinx(-cosx) - ∫(-cosx)(cosx) dx
This simplifies to:
∫sin²x dx = -sinxcosx + ∫cos²x dx
Now, we use the Pythagorean identity: cos²x = 1 - sin²x
∫sin²x dx = -sinxcosx + ∫(1 - sin²x) dx
∫sin²x dx = -sinxcosx + ∫1 dx - ∫sin²x dx
Notice that the integral of sin²x appears on both sides of the equation. We can solve for it algebraically:
2∫sin²x dx = -sinxcosx + x
∫sin²x dx = x/2 - (1/2)sinxcosx + C
While this solution looks different from the one obtained using the power-reducing formula, it is actually equivalent. Using the double-angle formula for sine (sin(2x) = 2sinxcosx), we can verify the equivalence of the two solutions.
Understanding the Constant of Integration (C)
The constant of integration, C, is crucial in indefinite integrals. It represents a family of functions, each differing by a constant, that all have the same derivative (sin²x in this case). The value of C is determined by specific boundary conditions or initial values if the problem involves a definite integral.
Definite Integrals of Sin²x
When dealing with definite integrals, we evaluate the antiderivative at the upper and lower limits of integration and find the difference. For example:
∫(from 0 to π) sin²x dx = = (π/2 - 0) - (0 - 0) = π/2
This shows that the area under the curve of sin²x from 0 to π is π/2.
Applications of the Integral of Sin²x
The integral of sin²x finds widespread application in various fields, including:
- Physics: Calculating average power in alternating current circuits, analyzing wave phenomena, and solving problems in oscillatory motion.
- Engineering: Analyzing vibrations, designing signal processing systems, and solving differential equations in structural mechanics.
- Probability and Statistics: Involving probability distributions and statistical calculations.
Frequently Asked Questions (FAQ)
-
Q: Can I use other trigonometric identities to solve this integral? A: Yes, several other identities could be used, but the power-reducing formula offers the most straightforward approach. Integration by parts, as shown, is another valid method, though less efficient.
-
Q: What if I have sin²(ax) instead of sin²(x)? A: A simple u-substitution will handle this. Let u = ax, then du = a dx. The integral becomes (1/a)∫sin²(u) du, which can then be solved using the methods discussed above.
-
Q: How do I integrate other powers of sin x, like sin³x or sin⁴x? A: For higher powers, you will often need to use reduction formulas or a combination of trigonometric identities and integration techniques. These become increasingly more complex.
Conclusion
The integration of sin²x, while initially appearing daunting, is readily solvable using the power-reducing formula or integration by parts. Understanding the underlying trigonometric identities and applying appropriate integration techniques is key. This guide has provided a comprehensive walkthrough, clarifying the methods and their applications. Remember the importance of the constant of integration and the versatility of these techniques in various scientific and engineering contexts. Mastering this integral opens doors to understanding more complex problems involving trigonometric functions and strengthens your foundation in calculus. Practice is crucial; work through various examples and build your confidence in tackling these types of integrals.
Latest Posts
Latest Posts
-
Candy Of Mice And Men
Sep 11, 2025
-
Property For Sale Sandbanks Dorset
Sep 11, 2025
-
Alenia Aermacchi M 346 Master
Sep 11, 2025
-
Thank You For Listening Gif
Sep 11, 2025
-
Most Beautiful Capitals In World
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Integration Of Sin Squared X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.