Gcf Of 90 And 252
letscamok
Sep 01, 2025 · 6 min read
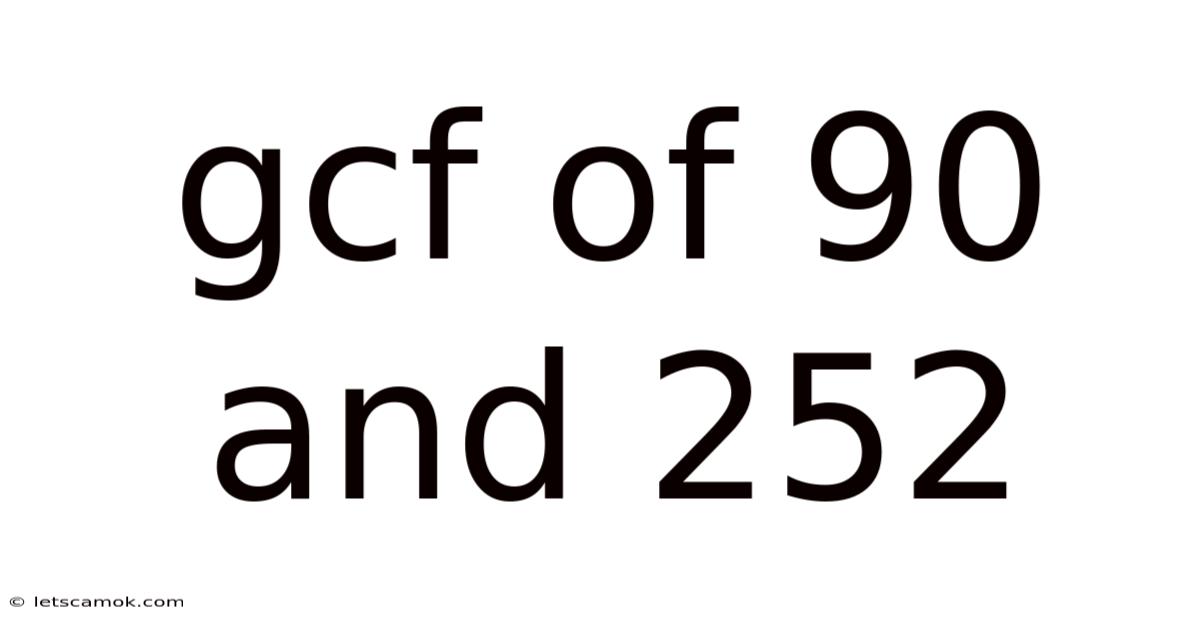
Table of Contents
Finding the Greatest Common Factor (GCF) of 90 and 252: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will explore multiple methods for determining the GCF of 90 and 252, providing a detailed explanation suitable for students of various levels. We'll delve into the underlying principles, illustrate different approaches, and answer frequently asked questions to solidify your understanding of this important mathematical concept. This comprehensive guide will equip you with the skills to tackle similar problems with confidence.
Understanding Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 90 and 252, let's establish a clear understanding of what the GCF represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. This concept is crucial in various mathematical applications, including simplifying fractions, solving algebraic equations, and understanding number theory.
Method 1: Prime Factorization
This method is a reliable and conceptually strong approach to finding the GCF. It involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of 90:
We can start by dividing 90 by the smallest prime number, 2: 90 ÷ 2 = 45. 45 is not divisible by 2, so we move to the next prime number, 3: 45 ÷ 3 = 15. 15 is also divisible by 3: 15 ÷ 3 = 5. 5 is a prime number, so we stop here. Therefore, the prime factorization of 90 is 2 × 3 × 3 × 5, or 2¹ × 3² × 5¹.
-
Find the prime factorization of 252:
Let's start with 2: 252 ÷ 2 = 126. 126 is also divisible by 2: 126 ÷ 2 = 63. 63 is not divisible by 2, but it is divisible by 3: 63 ÷ 3 = 21. 21 is also divisible by 3: 21 ÷ 3 = 7. 7 is a prime number. Therefore, the prime factorization of 252 is 2 × 2 × 3 × 3 × 7, or 2² × 3² × 7¹.
-
Identify common factors:
Now, compare the prime factorizations of 90 and 252:
90 = 2¹ × 3² × 5¹ 252 = 2² × 3² × 7¹
The common factors are 2¹ and 3².
-
Calculate the GCF:
Multiply the common factors together: 2¹ × 3² = 2 × 9 = 18.
Therefore, the GCF of 90 and 252 is 18.
Method 2: Listing Factors
This method is straightforward, particularly for smaller numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Steps:
-
List the factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
-
List the factors of 252: 1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252
-
Identify common factors: Compare the two lists. The common factors are 1, 2, 3, 6, 9, and 18.
-
Determine the GCF: The largest common factor is 18.
Therefore, the GCF of 90 and 252 is 18. This method becomes less efficient with larger numbers, making the prime factorization method more practical in those cases.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is an efficient method for finding the GCF, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
-
Start with the larger number (252) and the smaller number (90):
-
Repeatedly apply the division algorithm:
- 252 ÷ 90 = 2 with a remainder of 72.
- 90 ÷ 72 = 1 with a remainder of 18.
- 72 ÷ 18 = 4 with a remainder of 0.
-
The GCF is the last non-zero remainder: The last non-zero remainder is 18.
Therefore, the GCF of 90 and 252 is 18. The Euclidean Algorithm provides a systematic and efficient way to find the GCF, even for very large numbers.
The Importance of GCF in Mathematics and Beyond
Understanding and calculating the GCF isn't just an academic exercise; it has practical applications across various fields:
-
Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For example, the fraction 90/252 can be simplified by dividing both the numerator and denominator by their GCF (18), resulting in the equivalent fraction 5/14.
-
Algebra: The GCF is used to factor algebraic expressions, making them easier to solve and analyze.
-
Geometry: The concept is applied in geometric problems involving area calculations and finding common dimensions.
-
Computer Science: The Euclidean Algorithm, used to find the GCF, is a fundamental algorithm in computer science and cryptography.
-
Music Theory: The GCF plays a role in determining musical intervals and harmonies.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, they are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF of two numbers be larger than the smaller number?
A: No, the GCF of two numbers can never be larger than the smaller of the two numbers.
Q: Is there a way to find the GCF of more than two numbers?
A: Yes, you can extend the methods discussed above to find the GCF of more than two numbers. For prime factorization, you would find the prime factorization of each number and then identify the common factors with the lowest exponent. For the Euclidean algorithm, you would iteratively find the GCF of pairs of numbers until you get the GCF of all the numbers.
Q: What if one of the numbers is zero?
A: The GCF of any number and zero is the number itself (excluding the case where both numbers are zero; in that case, the GCF is undefined).
Q: Are there any online calculators to verify my GCF calculations?
A: While I cannot provide links to external websites, a simple online search for "greatest common factor calculator" will reveal numerous resources that can help you check your work.
Conclusion
Finding the greatest common factor is a valuable skill with broad applications in mathematics and beyond. We've explored three distinct methods: prime factorization, listing factors, and the Euclidean Algorithm. Each method offers a unique approach, with the Euclidean algorithm providing a particularly efficient solution for larger numbers. Mastering these techniques will enhance your mathematical understanding and problem-solving capabilities. Remember to choose the method that best suits your needs and the complexity of the problem at hand. By understanding the underlying principles and practicing these methods, you'll confidently tackle GCF calculations and appreciate their significance in various mathematical contexts.
Latest Posts
Latest Posts
-
A Minor On Piano Chord
Sep 01, 2025
-
Insects That Look Like Ticks
Sep 01, 2025
-
Hermione Granger Punches Draco Malfoy
Sep 01, 2025
-
Year 1 Reading Comprehension Pdf
Sep 01, 2025
-
What Is An Inglenook Fireplace
Sep 01, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 90 And 252 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.