1/2 A B Sin C
letscamok
Sep 19, 2025 · 6 min read
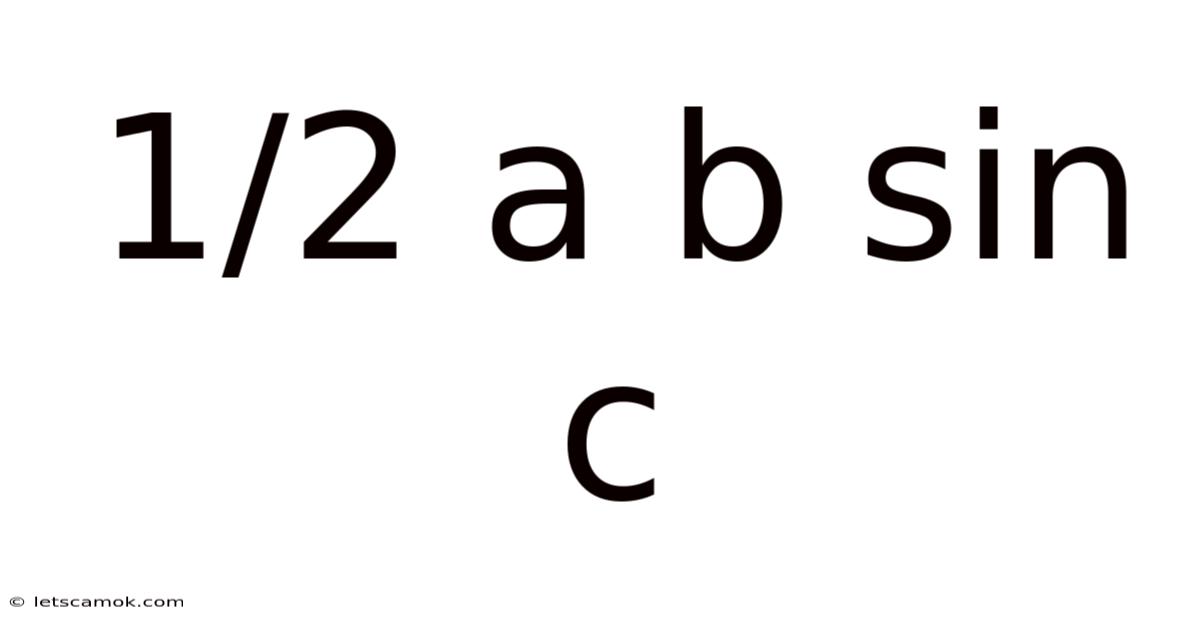
Table of Contents
Understanding the 1/2absinC Formula: Area of a Triangle
The formula ½absinC is a fundamental concept in trigonometry used to calculate the area of a triangle. This seemingly simple equation unlocks a powerful tool for solving various geometric problems, moving beyond the basic base times height divided by two approach. This article will provide a comprehensive explanation of the formula, exploring its derivation, applications, and practical examples. We'll delve into the underlying principles, ensuring a solid understanding for learners of all levels, from high school geometry to advanced mathematical applications. Let's unlock the power of this crucial trigonometric tool.
Introduction: Beyond the Basics of Triangle Area
Most of us are familiar with the basic formula for calculating the area of a triangle: Area = ½ * base * height. This formula is intuitive and works well when the height is readily available. However, what if you only know the lengths of two sides and the angle between them? This is where the ½absinC formula shines. It provides an elegant and efficient method for calculating the area when the height is unknown or difficult to determine. This formula is especially useful in surveying, engineering, and various fields requiring precise area calculations in scenarios where direct measurement of height is impractical.
Deriving the ½absinC Formula
To understand this formula, let's visualize a triangle ABC, where 'a' and 'b' represent the lengths of two sides, and 'C' is the angle between them. We can derive the ½absinC formula using a combination of geometry and trigonometry.
-
Constructing the Altitude: Draw an altitude (height) from vertex B to side AC, and label the point where the altitude intersects AC as D. This altitude creates two right-angled triangles: ABD and CBD.
-
Applying Trigonometry: In right-angled triangle ABD, we can use the definition of sine: sinA = opposite/hypotenuse. In our context, sinC = BD/a (where BD is the height of the triangle). Therefore, BD = a * sinC.
-
Calculating the Area: Now we can use the basic area formula: Area = ½ * base * height. In our triangle, the base is 'b' and the height is 'BD', which we've determined to be 'a * sinC'. Substituting this into the area formula, we get: Area = ½ * b * (a * sinC) = ½absinC.
Understanding the Components of the Formula
-
a and b: These represent the lengths of two sides of the triangle. It is crucial to remember that these are the sides adjacent to angle C.
-
C: This represents the angle between sides 'a' and 'b'. It's essential to use the angle in degrees or radians, depending on your calculator settings. Using the wrong units will lead to incorrect results.
-
sinC: This is the sine of angle C. The sine function is a trigonometric ratio that relates the angle to the ratio of the opposite side and hypotenuse in a right-angled triangle. It's a fundamental concept in trigonometry and is readily available on most calculators.
-
½: This constant factor simply reflects that the area of a triangle is half the area of a rectangle with the same base and height.
Practical Applications of the ½absinC Formula
The ½absinC formula finds applications in a wide range of fields, including:
-
Surveying: Determining the area of land parcels based on measured side lengths and angles. This is crucial for property boundaries, construction projects, and land management.
-
Navigation: Calculating distances and areas on maps and charts. This is particularly important in maritime and aviation navigation.
-
Engineering: Calculating areas of irregular shapes, which are often broken down into triangles for simpler calculations. This finds use in structural analysis, bridge design, and other civil engineering tasks.
-
Computer Graphics: Generating realistic images and 3D models often requires precise area calculations for various polygons, with triangles being fundamental building blocks.
-
Physics: The formula can be applied in vector calculations and physics problems involving forces and angles.
Step-by-Step Example Calculation
Let's work through a concrete example to solidify our understanding. Suppose we have a triangle with sides a = 10 cm, b = 8 cm, and the angle C = 60°. Let's calculate its area:
-
Identify the values: a = 10 cm, b = 8 cm, C = 60°.
-
Calculate sinC: sin(60°) = 0.866 (approximately). You can use a scientific calculator for this.
-
Apply the formula: Area = ½ * 10 cm * 8 cm * 0.866 = 34.64 cm².
Therefore, the area of the triangle is approximately 34.64 square centimeters.
Using the Formula with Different Angles
The formula remains consistent regardless of the type of triangle (acute, obtuse, or right-angled). The sine function handles the different angles appropriately. For example:
-
Acute Triangle (C < 90°): sinC will be a positive value between 0 and 1.
-
Obtuse Triangle (C > 90°): sinC will still be a positive value between 0 and 1 (sine is positive in the second quadrant).
-
Right-angled Triangle (C = 90°): sin(90°) = 1. The formula simplifies to ½ab, which is equivalent to the basic area formula using legs as base and height.
Common Mistakes and Troubleshooting
-
Incorrect Unit Conversion: Ensure consistency in units (e.g., all measurements in centimeters or meters). Mixing units will lead to inaccurate results.
-
Calculator Settings: Double-check that your calculator is set to the correct angle mode (degrees or radians) before calculating sinC.
-
Angle Identification: Make sure you are using the correct angle (the angle between sides 'a' and 'b').
Frequently Asked Questions (FAQ)
Q: Can I use this formula for any triangle?
A: Yes, the ½absinC formula is applicable to any triangle, regardless of its type (acute, obtuse, or right-angled).
Q: What if I only know one side and two angles?
A: You can use the sine rule or cosine rule to find the length of another side first, then apply the ½absinC formula.
Q: Is there an alternative formula for calculating triangle area?
A: Yes, Heron's formula is another method, particularly useful when you know the lengths of all three sides. However, ½absinC is more straightforward when you know two sides and the included angle.
Q: What if the angle C is 0° or 180°?
A: If C = 0° or 180°, the triangle is degenerate (it's a straight line), and its area is 0. This is reflected in the formula because sin(0°) = sin(180°) = 0.
Conclusion: Mastering the ½absinC Formula
The ½absinC formula is a valuable tool in various mathematical and practical applications. Its elegant derivation from basic geometry and trigonometry makes it a powerful yet accessible concept. By understanding its components, applications, and potential pitfalls, you can confidently use this formula to solve a wide range of area calculation problems, expanding your problem-solving capabilities in geometry and related fields. Mastering this formula opens doors to a deeper understanding of trigonometry and its applications in diverse areas. Remember to practice consistently, applying the formula to various triangle examples to solidify your understanding and build your confidence in tackling complex geometric problems.
Latest Posts
Latest Posts
-
Motor Relay And Sensory Neurons
Sep 20, 2025
-
Continuous Stirred Tank Reactor Cstr
Sep 20, 2025
-
Will Mascara Ruin Your Eyelashes
Sep 20, 2025
-
Lookup Social Media By Email
Sep 20, 2025
-
Pillow Plump Soap And Glory
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 1/2 A B Sin C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.